Exploratory Data Analysis (EDA) is the critical first step in any data analysis project. Before running statistical tests, fitting models, or drawing conclusions, you need to understand your data intimately. EDA is the practice of using visualization and summary statistics to explore datasets, uncover patterns, detect anomalies, test assumptions, and formulate hypotheses.
The term “Exploratory Data Analysis” was popularized by John Tukey in his groundbreaking 1977 book (Tukey 1977). Tukey emphasized that EDA is fundamentally different from confirmatory data analysis. While confirmatory analysis tests specific hypotheses with formal statistical procedures, exploratory analysis is open-ended, creative, and iterative. It is detective work—you are looking for clues about what your data can tell you.
“Exploratory data analysis is detective work—numerical detective work—or counting detective work—or graphical detective work… The most important maxim for data analysis is: ‘Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.’” — John Tukey
EDA serves several critical purposes:
EDA is not a one-time activity. You will return to exploratory analysis repeatedly throughout a project as you clean data, fit models, and interpret results. Each stage reveals new questions that send you back to explore further.
Effective exploratory analysis requires a particular mindset. Be curious but skeptical. Look for patterns but question them. Be systematic but flexible. Most importantly, resist the urge to jump immediately to statistical testing.
Start broad, then narrow. Begin with the big picture—what is the overall structure of your data? How many observations and variables? What are the basic distributions? Then zoom in on interesting features, unusual patterns, or potential problems.
Use multiple approaches. Never rely on a single summary statistic or plot type. Look at your data from many angles. A histogram might suggest normality that a Q-Q plot reveals as questionable. A correlation coefficient might suggest no relationship that a scatterplot shows is actually nonlinear.
Document your exploration. Keep notes about what you find, questions that arise, and decisions you make. This documentation serves both as a record for yourself and as the foundation for your eventual analysis narrative.
Trust your visual system. Humans are extraordinarily good at pattern detection. A well-designed plot can reveal relationships that summary statistics obscure. Anscombe’s Quartet demonstrated this dramatically—four datasets with identical means, variances, and correlations but completely different underlying patterns visible only through visualization (Figure 22.4).
The first step in any EDA is to understand the basic structure of your dataset. R provides several functions for getting an overview of your data.
The str() function shows the structure of an object:
# Load example dataset
data(iris)
# View structure
str(iris)'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...This reveals that iris has 150 observations of 5 variables: four numeric measurements and one factor. The glimpse() function from dplyr provides similar information in a more compact format:
glimpse(iris)Rows: 150
Columns: 5
$ Sepal.Length <dbl> 5.1, 4.9, 4.7, 4.6, 5.0, 5.4, 4.6, 5.0, 4.4, 4.9, 5.4, 4.…
$ Sepal.Width <dbl> 3.5, 3.0, 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.…
$ Petal.Length <dbl> 1.4, 1.4, 1.3, 1.5, 1.4, 1.7, 1.4, 1.5, 1.4, 1.5, 1.5, 1.…
$ Petal.Width <dbl> 0.2, 0.2, 0.2, 0.2, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.2, 0.…
$ Species <fct> setosa, setosa, setosa, setosa, setosa, setosa, setosa, s…The summary() function provides basic statistics for each variable:
summary(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
Median :5.800 Median :3.000 Median :4.350 Median :1.300
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Species
setosa :50
versicolor:50
virginica :50
For numeric variables, summary() returns the minimum, first quartile, median, mean, third quartile, and maximum. For factors, it shows counts for each level.
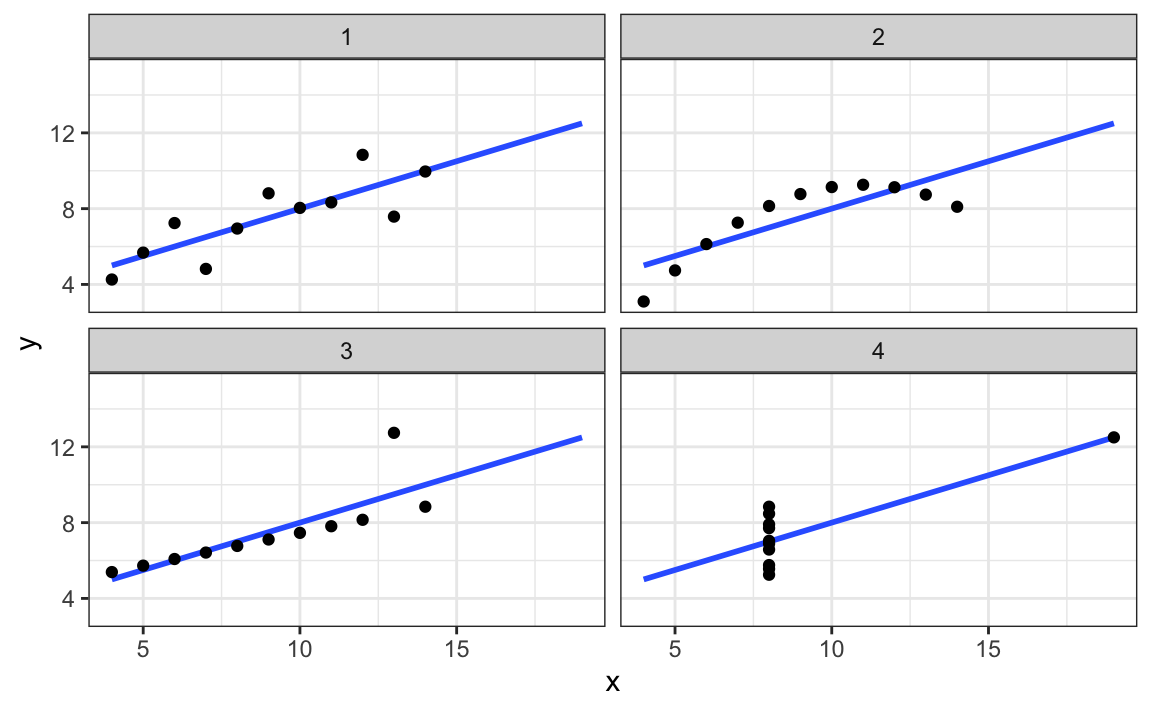Always verify the dimensions of your data:
# Number of rows and columns
dim(iris)[1] 150 5# Number of rows
nrow(iris)[1] 150# Number of columns
ncol(iris)[1] 5# Column names
names(iris)[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species" # Column types
sapply(iris, class)Sepal.Length Sepal.Width Petal.Length Petal.Width Species
"numeric" "numeric" "numeric" "numeric" "factor" Missing data is common and can profoundly affect your analysis. Check for missing values systematically:
# Check for any missing values
any(is.na(iris))[1] FALSE# Count missing values per column
colSums(is.na(iris))Sepal.Length Sepal.Width Petal.Length Petal.Width Species
0 0 0 0 0 # Visualize missing data pattern (using a dataset with missing values)
# Create example data with missing values
iris_missing <- iris
iris_missing[sample(1:150, 10), "Sepal.Length"] <- NA
iris_missing[sample(1:150, 5), "Petal.Width"] <- NA
# Summary of missing values
colSums(is.na(iris_missing))Sepal.Length Sepal.Width Petal.Length Petal.Width Species
10 0 0 5 0 When you find missing values, ask: Are they missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR)? The pattern of missingness affects how you should handle it. Never blindly delete rows with missing data without understanding why values are missing.
After understanding the basic structure, examine each variable individually. Univariate analysis reveals the distribution, central tendency, spread, and anomalies in single variables.
For continuous variables, visualize the distribution using histograms, density plots, and boxplots.
Histograms show the frequency of values in bins:
ggplot(iris, aes(x = Sepal.Length)) +
geom_histogram(bins = 20, fill = "steelblue", color = "white") +
labs(x = "Sepal Length (cm)",
y = "Count",
title = "Distribution of Sepal Length") +
theme_minimal()
Density plots provide a smooth estimate of the distribution:
ggplot(iris, aes(x = Sepal.Length)) +
geom_density(fill = "coral", alpha = 0.5) +
labs(x = "Sepal Length (cm)",
y = "Density",
title = "Density Plot of Sepal Length") +
theme_minimal()
Boxplots summarize the distribution using quartiles and identify potential outliers:
ggplot(iris, aes(y = Sepal.Length)) +
geom_boxplot(fill = "lightgreen") +
labs(y = "Sepal Length (cm)",
title = "Boxplot of Sepal Length") +
theme_minimal()
You can compare distributions of multiple variables using faceted plots:
iris |>
pivot_longer(cols = -Species,
names_to = "measurement",
values_to = "value") |>
ggplot(aes(x = value, fill = measurement)) +
geom_histogram(bins = 20, color = "white", show.legend = FALSE) +
facet_wrap(~measurement, scales = "free") +
labs(x = "Measurement (cm)",
y = "Count",
title = "Distributions of Iris Measurements") +
theme_minimal()
For categorical variables, use bar charts and frequency tables.
ggplot(iris, aes(x = Species, fill = Species)) +
geom_bar(show.legend = FALSE) +
labs(x = "Species",
y = "Count",
title = "Distribution of Iris Species") +
theme_minimal()
Frequency tables provide the same information numerically:
# Frequency table
table(iris$Species)
setosa versicolor virginica
50 50 50 # Proportions
prop.table(table(iris$Species))
setosa versicolor virginica
0.3333333 0.3333333 0.3333333 Calculate summary statistics to quantify central tendency and spread:
# Mean and median
mean(iris$Sepal.Length)[1] 5.843333median(iris$Sepal.Length)[1] 5.8# Standard deviation and variance
sd(iris$Sepal.Length)[1] 0.8280661var(iris$Sepal.Length)[1] 0.6856935# Interquartile range
IQR(iris$Sepal.Length)[1] 1.3# Range
range(iris$Sepal.Length)[1] 4.3 7.9# Quantiles
quantile(iris$Sepal.Length, probs = c(0.25, 0.50, 0.75))25% 50% 75%
5.1 5.8 6.4 # Summary statistics for all numeric variables
iris |>
select(where(is.numeric)) |>
summary() Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
Median :5.800 Median :3.000 Median :4.350 Median :1.300
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500 You can also calculate summary statistics by group:
iris |>
group_by(Species) |>
summarize(
n = n(),
mean_sepal = mean(Sepal.Length),
sd_sepal = sd(Sepal.Length),
median_sepal = median(Sepal.Length),
iqr_sepal = IQR(Sepal.Length)
)# A tibble: 3 × 6
Species n mean_sepal sd_sepal median_sepal iqr_sepal
<fct> <int> <dbl> <dbl> <dbl> <dbl>
1 setosa 50 5.01 0.352 5 0.400
2 versicolor 50 5.94 0.516 5.9 0.7
3 virginica 50 6.59 0.636 6.5 0.675After understanding individual variables, explore relationships between pairs of variables. The appropriate visualization depends on the types of variables being compared.
For two continuous variables, scatterplots are the primary tool:
ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width)) +
geom_point(alpha = 0.6, size = 2) +
geom_smooth(method = "lm", se = TRUE, color = "red") +
labs(x = "Sepal Length (cm)",
y = "Sepal Width (cm)",
title = "Relationship Between Sepal Dimensions") +
theme_minimal()
Add color to reveal group patterns:
ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, color = Species)) +
geom_point(alpha = 0.7, size = 2.5) +
labs(x = "Sepal Length (cm)",
y = "Sepal Width (cm)",
title = "Sepal Dimensions by Species") +
theme_minimal()
Calculate correlation coefficients to quantify linear relationships:
# Pearson correlation
cor(iris$Sepal.Length, iris$Sepal.Width)[1] -0.1175698# Correlation matrix for all numeric variables
iris |>
select(where(is.numeric)) |>
cor() Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000Correlation measures the strength of linear association between variables, but it does not imply causation. Two variables may be correlated because one causes the other, because both are caused by a third variable, or purely by chance. Always examine scatterplots—correlation coefficients can be misleading for nonlinear relationships.
Create a correlation plot matrix to view all pairwise relationships:
# Using GGally package for pairs plot
if (!require(GGally)) install.packages("GGally")
library(GGally)
ggpairs(iris,
columns = 1:4,
aes(color = Species, alpha = 0.5),
upper = list(continuous = "cor"),
lower = list(continuous = "points")) +
theme_minimal()
For a continuous variable across categorical groups, use boxplots or violin plots:
ggplot(iris, aes(x = Species, y = Sepal.Length, fill = Species)) +
geom_boxplot(alpha = 0.7, show.legend = FALSE) +
labs(x = "Species",
y = "Sepal Length (cm)",
title = "Sepal Length by Species") +
theme_minimal()
Violin plots combine density plots and boxplots to show the full distribution:
ggplot(iris, aes(x = Species, y = Sepal.Length, fill = Species)) +
geom_violin(alpha = 0.7, show.legend = FALSE) +
geom_boxplot(width = 0.2, alpha = 0.5, show.legend = FALSE) +
labs(x = "Species",
y = "Sepal Length (cm)",
title = "Sepal Length Distribution by Species") +
theme_minimal()
You can also use overlapping density plots:
ggplot(iris, aes(x = Sepal.Length, fill = Species)) +
geom_density(alpha = 0.5) +
labs(x = "Sepal Length (cm)",
y = "Density",
title = "Sepal Length Distribution by Species") +
theme_minimal()
For two categorical variables, use contingency tables and mosaic plots.
# Create example categorical data using mpg dataset
data(mpg)
# Contingency table
table(mpg$class, mpg$drv)
4 f r
2seater 0 0 5
compact 12 35 0
midsize 3 38 0
minivan 0 11 0
pickup 33 0 0
subcompact 4 22 9
suv 51 0 11# Proportions
prop.table(table(mpg$class, mpg$drv))
4 f r
2seater 0.00000000 0.00000000 0.02136752
compact 0.05128205 0.14957265 0.00000000
midsize 0.01282051 0.16239316 0.00000000
minivan 0.00000000 0.04700855 0.00000000
pickup 0.14102564 0.00000000 0.00000000
subcompact 0.01709402 0.09401709 0.03846154
suv 0.21794872 0.00000000 0.04700855Visualize with a stacked or grouped bar chart:
ggplot(mpg, aes(x = class, fill = drv)) +
geom_bar(position = "dodge") +
labs(x = "Vehicle Class",
y = "Count",
fill = "Drive Type",
title = "Vehicle Class by Drive Type") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
Mosaic plots show the relative proportions:
if (!require(ggmosaic)) install.packages("ggmosaic")Error in `contrib.url()`:
! trying to use CRAN without setting a mirrorlibrary(ggmosaic)Error in `library()`:
! there is no package called 'ggmosaic'ggplot(mpg) +
geom_mosaic(aes(x = product(drv, class), fill = drv)) +
labs(x = "Vehicle Class",
y = "Drive Type",
title = "Mosaic Plot: Class vs Drive Type") +
theme_minimal()Error in `geom_mosaic()`:
! could not find function "geom_mosaic"Outliers are observations that differ markedly from other observations in the dataset. They may represent errors, rare but valid extreme values, or the most interesting part of your data. Never automatically delete outliers—investigate them.
Boxplots automatically flag potential outliers (values beyond 1.5 × IQR from the quartiles):
ggplot(iris, aes(y = Sepal.Width)) +
geom_boxplot(fill = "lightblue") +
labs(y = "Sepal Width (cm)",
title = "Potential Outliers in Sepal Width") +
theme_minimal()
Scatterplots reveal multivariate outliers:
# Calculate z-scores to identify outliers
iris_z <- iris |>
mutate(
z_sepal_length = scale(Sepal.Length),
z_sepal_width = scale(Sepal.Width),
is_outlier = abs(z_sepal_length) > 2.5 | abs(z_sepal_width) > 2.5
)
ggplot(iris_z, aes(x = Sepal.Length, y = Sepal.Width, color = is_outlier)) +
geom_point(size = 2.5, alpha = 0.7) +
scale_color_manual(values = c("FALSE" = "steelblue", "TRUE" = "red"),
labels = c("Normal", "Potential Outlier")) +
labs(x = "Sepal Length (cm)",
y = "Sepal Width (cm)",
color = "Status",
title = "Outlier Detection Using Z-scores") +
theme_minimal()
Several statistical methods identify outliers:
# Z-score method (values > 3 SD from mean)
z_scores <- scale(iris$Sepal.Length)
outliers_z <- which(abs(z_scores) > 3)
cat("Outliers using z-score method:", outliers_z, "\n")Outliers using z-score method: # IQR method (values beyond 1.5 × IQR from quartiles)
Q1 <- quantile(iris$Sepal.Length, 0.25)
Q3 <- quantile(iris$Sepal.Length, 0.75)
IQR_val <- Q3 - Q1
lower_bound <- Q1 - 1.5 * IQR_val
upper_bound <- Q3 + 1.5 * IQR_val
outliers_iqr <- which(iris$Sepal.Length < lower_bound |
iris$Sepal.Length > upper_bound)
cat("Outliers using IQR method:", outliers_iqr, "\n")Outliers using IQR method: When you identify outliers, ask:
Document your decisions about outlier handling.
When outliers are present, the mean and standard deviation can be heavily influenced by extreme values. Robust statistics provide alternatives that are less sensitive to outliers.
Median vs Mean: The median is the value that splits the data in half—50% above, 50% below. Unlike the mean, the median is unaffected by extreme values.
MAD vs Standard Deviation: The Median Absolute Deviation (MAD) is a robust measure of spread. It is calculated as the median of the absolute deviations from the median:
\[\text{MAD} = \text{median}(|X_i - \text{median}(X)|)\]
To make MAD comparable to the standard deviation for normally distributed data, it is often scaled by a factor of 1.4826:
\[\text{MAD}_{\text{scaled}} = 1.4826 \times \text{MAD}\]
# Compare robust and non-robust statistics
# Create data with an outlier
normal_data <- c(rnorm(99, mean = 50, sd = 5), 200) # One extreme outlier
# Non-robust statistics
cat("Mean:", round(mean(normal_data), 2), "\n")Mean: 51.74 cat("SD:", round(sd(normal_data), 2), "\n")SD: 15.8 # Robust statistics
cat("Median:", round(median(normal_data), 2), "\n")Median: 49.78 cat("MAD (scaled):", round(mad(normal_data), 2), "\n")MAD (scaled): 4.58 # IQR is also robust
cat("IQR:", round(IQR(normal_data), 2), "\n")IQR: 6.06 The MAD and IQR give sensible estimates of spread that are not inflated by the single outlier.
The boxplot outlier rule (1.5 × IQR from the quartiles) is known as Tukey’s fences. Values outside the inner fences (1.5 × IQR) are considered potential outliers, while values outside the outer fences (3 × IQR) are considered extreme outliers. This rule is robust because it is based on quartiles rather than the mean and standard deviation.
# Calculate Tukey's fences
Q1 <- quantile(normal_data, 0.25)
Q3 <- quantile(normal_data, 0.75)
IQR_val <- Q3 - Q1
inner_fence_lower <- Q1 - 1.5 * IQR_val
inner_fence_upper <- Q3 + 1.5 * IQR_val
outer_fence_lower <- Q1 - 3 * IQR_val
outer_fence_upper <- Q3 + 3 * IQR_val
cat("Inner fences:", round(inner_fence_lower, 2), "to", round(inner_fence_upper, 2), "\n")Inner fences: 37.96 to 62.21 cat("Outer fences:", round(outer_fence_lower, 2), "to", round(outer_fence_upper, 2), "\n")Outer fences: 28.87 to 71.3 cat("Outlier value:", max(normal_data), "- far beyond outer fence\n")Outlier value: 200 - far beyond outer fenceBeyond outliers, perform systematic quality checks to identify problems in your data.
Duplicate records can skew your analysis:
# Check for completely duplicated rows
any(duplicated(iris))[1] TRUE# Find duplicated rows
iris[duplicated(iris), ] Sepal.Length Sepal.Width Petal.Length Petal.Width Species
143 5.8 2.7 5.1 1.9 virginica# Remove duplicates (if appropriate)
iris_unique <- distinct(iris)Check that values fall within plausible ranges:
# Check for negative values (impossible for lengths)
iris |>
select(where(is.numeric)) |>
summarize(across(everything(),
list(min = min, max = max))) Sepal.Length_min Sepal.Length_max Sepal.Width_min Sepal.Width_max
1 4.3 7.9 2 4.4
Petal.Length_min Petal.Length_max Petal.Width_min Petal.Width_max
1 1 6.9 0.1 2.5# Flag implausible values
iris |>
filter(Sepal.Length < 0 | Sepal.Length > 100) |>
nrow()[1] 0Look for logical inconsistencies:
# Example: petal length should not exceed sepal length
iris |>
filter(Petal.Length > Sepal.Length) |>
select(Species, Sepal.Length, Petal.Length)[1] Species Sepal.Length Petal.Length
<0 rows> (or 0-length row.names)# Check for impossible combinations
# (This dataset has none, but the pattern is important)Effective EDA follows a systematic workflow. While the specific steps vary by project, a general framework includes:
1. Load and inspect the data - Read the data into R - Check dimensions, structure, and variable types - Examine the first and last few rows
2. Check data quality - Identify missing values - Look for duplicates - Validate ranges and consistency
3. Univariate analysis - Examine each variable individually - Create appropriate visualizations - Calculate summary statistics
4. Bivariate and multivariate analysis - Explore relationships between variables - Create scatterplots, correlation matrices, and grouped comparisons - Look for patterns, clusters, and anomalies
5. Identify and investigate anomalies - Detect outliers using visual and statistical methods - Investigate unusual patterns - Document decisions about data handling
6. Formulate questions and hypotheses - Based on patterns observed, what questions arise? - What hypotheses warrant testing? - What further analyses are needed?
7. Document findings - Summarize key characteristics of the data - Note data quality issues and how you addressed them - Record interesting patterns and potential analyses
Let’s apply this workflow to a real dataset:
# Load data
data(mpg)
# 1. Inspect
glimpse(mpg)Rows: 234
Columns: 11
$ manufacturer <chr> "audi", "audi", "audi", "audi", "audi", "audi", "audi", "…
$ model <chr> "a4", "a4", "a4", "a4", "a4", "a4", "a4", "a4 quattro", "…
$ displ <dbl> 1.8, 1.8, 2.0, 2.0, 2.8, 2.8, 3.1, 1.8, 1.8, 2.0, 2.0, 2.…
$ year <int> 1999, 1999, 2008, 2008, 1999, 1999, 2008, 1999, 1999, 200…
$ cyl <int> 4, 4, 4, 4, 6, 6, 6, 4, 4, 4, 4, 6, 6, 6, 6, 6, 6, 8, 8, …
$ trans <chr> "auto(l5)", "manual(m5)", "manual(m6)", "auto(av)", "auto…
$ drv <chr> "f", "f", "f", "f", "f", "f", "f", "4", "4", "4", "4", "4…
$ cty <int> 18, 21, 20, 21, 16, 18, 18, 18, 16, 20, 19, 15, 17, 17, 1…
$ hwy <int> 29, 29, 31, 30, 26, 26, 27, 26, 25, 28, 27, 25, 25, 25, 2…
$ fl <chr> "p", "p", "p", "p", "p", "p", "p", "p", "p", "p", "p", "p…
$ class <chr> "compact", "compact", "compact", "compact", "compact", "c…# 2. Check quality
colSums(is.na(mpg))manufacturer model displ year cyl trans
0 0 0 0 0 0
drv cty hwy fl class
0 0 0 0 0 # 3. Univariate analysis
summary(mpg |> select(where(is.numeric))) displ year cyl cty hwy
Min. :1.600 Min. :1999 Min. :4.000 Min. : 9.00 Min. :12.00
1st Qu.:2.400 1st Qu.:1999 1st Qu.:4.000 1st Qu.:14.00 1st Qu.:18.00
Median :3.300 Median :2004 Median :6.000 Median :17.00 Median :24.00
Mean :3.472 Mean :2004 Mean :5.889 Mean :16.86 Mean :23.44
3rd Qu.:4.600 3rd Qu.:2008 3rd Qu.:8.000 3rd Qu.:19.00 3rd Qu.:27.00
Max. :7.000 Max. :2008 Max. :8.000 Max. :35.00 Max. :44.00 # 4. Bivariate analysisp1 <- ggplot(mpg, aes(x = displ, y = hwy)) +
geom_point(alpha = 0.5) +
geom_smooth(method = "lm", se = FALSE, color = "red") +
labs(x = "Engine Displacement (L)",
y = "Highway MPG",
title = "Fuel Efficiency vs Engine Size") +
theme_minimal()
p2 <- ggplot(mpg, aes(x = class, y = hwy, fill = class)) +
geom_boxplot(show.legend = FALSE) +
labs(x = "Vehicle Class",
y = "Highway MPG",
title = "Fuel Efficiency by Class") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
p1 + p2
# 5. Key findings
mpg |>
group_by(class) |>
summarize(
n = n(),
mean_hwy = mean(hwy),
mean_cty = mean(cty),
mean_displ = mean(displ)
) |>
arrange(desc(mean_hwy))# A tibble: 7 × 5
class n mean_hwy mean_cty mean_displ
<chr> <int> <dbl> <dbl> <dbl>
1 compact 47 28.3 20.1 2.33
2 subcompact 35 28.1 20.4 2.66
3 midsize 41 27.3 18.8 2.92
4 2seater 5 24.8 15.4 6.16
5 minivan 11 22.4 15.8 3.39
6 suv 62 18.1 13.5 4.46
7 pickup 33 16.9 13 4.42Load the mtcars dataset and perform a basic inspection:
str() and glimpse()# Your code here
data(mtcars)Using the mtcars dataset:
mpg with an appropriate number of binshp (horsepower)wt (weight)mpg# Your code hereCompare mpg across different numbers of cylinders (cyl):
cyl to a factor# Your code hereExplore the relationship between wt (weight) and mpg:
cyl to see if the relationship varies by cylinder count# Your code hereIdentify potential outliers in the mtcars dataset:
hp to visually identify outliershpmpg and wt# Your code herePerform a complete EDA on the diamonds dataset (from ggplot2):
priceprice across different cut categoriescarat and price# Your code here
data(diamonds)Remember that EDA is iterative. Each discovery leads to new questions. Each visualization suggests another perspective. The goal is not to exhaustively analyze every possible relationship but to develop a deep understanding of your data that guides subsequent analysis and interpretation.
Exploratory Data Analysis is the foundation of sound statistical practice. Before testing hypotheses or fitting models, you must understand your data through systematic exploration. This chapter covered:
str(), glimpse(), and summary() to understand your dataThe techniques in this chapter will serve you in every data analysis project. Make EDA a habit—your statistical conclusions will be more reliable, your interpretations more nuanced, and your communication more convincing when they are grounded in thorough exploratory analysis.