Modern biology generates datasets with many variables: gene expression across thousands of genes, metabolomic profiles with hundreds of compounds, morphological measurements on many traits. When datasets have many variables, visualization becomes challenging and statistical analysis becomes complicated.
A typical machine learning challenge might include hundreds or thousands of predictors. For example, to compare each of the 784 features in a digit recognition problem, we would need to create 306,936 scatterplots! Creating a single scatter-plot of all the data is impossible due to the high dimensionality.
Dimensionality reduction creates a smaller set of new variables that capture most of the information in the original data. The general idea is to reduce the dimension of the dataset while preserving important characteristics, such as the distance between features or observations. These techniques help us:
Principal Component Analysis (PCA) (Pearson 1901; Hotelling 1933) is the most widely used dimensionality reduction technique. It finds new variables (principal components) that are linear combinations of the originals, chosen to capture maximum variance. The technique behind it—the singular value decomposition—is also useful in many other contexts.
Before diving into the mathematics, let’s build intuition with a simple example. Consider twin heights data where we have height measurements for 100 pairs of twins—some adults, some children.
set.seed(1988)
n <- 100
Sigma <- matrix(c(9, 9 * 0.9, 9 * 0.92, 9 * 1), 2, 2)
x <- rbind(mvrnorm(n / 2, c(69, 69), Sigma),
mvrnorm(n / 2, c(55, 55), Sigma))
lim <- c(48, 78)
rafalib::mypar()
plot(x, xlim = lim, ylim = lim,
xlab = "Twin 1 Height", ylab = "Twin 2 Height",
main = "Twin Heights: Adults and Children")
lines(x[c(1, 2), ], col = "blue", lwd = 2)
lines(x[c(2, 51), ], col = "red", lwd = 2)
points(x[c(1, 2, 51), ], pch = 16)
The scatterplot reveals high correlation and two clear groups: adults (upper right) and children (lower left). We can compute distances between observations:
d <- dist(x)
cat("Distance between observations 1 and 2:", round(as.matrix(d)[1, 2], 2), "\n")Distance between observations 1 and 2: 1.98 cat("Distance between observations 2 and 51:", round(as.matrix(d)[2, 51], 2), "\n")Distance between observations 2 and 51: 18.74 Now suppose we want to reduce from two dimensions to one while preserving these distances. A naive approach is to simply use one of the original variables:
z <- x[, 1]
rafalib::mypar()
plot(dist(x) / sqrt(2), dist(z),
xlab = "Original distance (scaled)", ylab = "One-dimension distance",
main = "Distance Approximation Using One Variable")
abline(0, 1, col = "red")
This works reasonably well, but we can do better. Notice that the variation in the data lies mostly along the diagonal. If we transform to the average and difference:
z <- cbind((x[, 2] + x[, 1]) / 2, x[, 2] - x[, 1])
rafalib::mypar()
plot(z, xlim = lim, ylim = lim - mean(lim),
xlab = "Average Height", ylab = "Difference",
main = "Transformed Coordinates")
lines(z[c(1, 2), ], col = "blue", lwd = 2)
lines(z[c(2, 51), ], col = "red", lwd = 2)
points(z[c(1, 2, 51), ], pch = 16)
Now the distances are mostly explained by the first dimension (the average). Using just this one dimension gives better distance approximation:
cat("Typical error with original variable:",
round(sd(dist(x) - dist(x[, 1]) * sqrt(2)), 2), "\n")Typical error with original variable: 1.21 cat("Typical error with average:",
round(sd(dist(x) - dist(z[, 1]) * sqrt(2)), 2), "\n")Typical error with average: 0.32 The average of the twin heights is essentially the first principal component! PCA finds these optimal linear combinations automatically.
Each row of the original matrix \(X\) was transformed using a linear transformation to create \(Z\):
\[Z_{i,1} = a_{1,1} X_{i,1} + a_{2,1} X_{i,2}\]
with \(a_{1,1} = 0.5\) and \(a_{2,1} = 0.5\) (the average).
In matrix notation: \[ Z = X A \mbox{ with } A = \begin{pmatrix} 1/2 & 1 \\ 1/2 & -1 \end{pmatrix} \]
Dimension reduction can be described as applying a transformation \(A\) to a matrix \(X\) that moves the information to the first few columns of \(Z = XA\), then keeping just these informative columns.
To preserve distances exactly, we need an orthogonal transformation—one where the columns of \(A\) have unit length and are perpendicular:
# Orthogonal transformation
z[, 1] <- (x[, 1] + x[, 2]) / sqrt(2)
z[, 2] <- (x[, 2] - x[, 1]) / sqrt(2)
# This preserves the original distances exactly
cat("Maximum distance difference:", max(abs(dist(z) - dist(x))), "\n")Maximum distance difference: 3.241851e-14 An orthogonal rotation preserves all distances while reorganizing the variance. Now most variance is in the first dimension:
qplot(z[, 1], bins = 20, color = I("black"), fill = I("steelblue")) +
labs(x = "First Principal Component", y = "Count",
title = "PC1 Separates Adults from Children")
The first PC clearly shows the two groups. We’ve reduced two dimensions to one with minimal information loss because the original variables were highly correlated:
cat("Correlation between twin heights:", round(cor(x[, 1], x[, 2]), 3), "\n")Correlation between twin heights: 0.988 cat("Correlation between PCs:", round(cor(z[, 1], z[, 2]), 3), "\n")Correlation between PCs: 0.088 The mathematical foundation involves eigenanalysis: decomposing the covariance (or correlation) matrix to find directions of maximum variation. For a detailed treatment of eigenvalues, eigenvectors, and their interpretation, see Section 52.9.
Given a covariance matrix \(\Sigma\), eigenanalysis finds:
The first principal component points in the direction of maximum variance. Each subsequent component is orthogonal (uncorrelated) and captures remaining variance in decreasing order.
The total variability can be defined as the sum of variances: \[ v_1 + v_2 + \cdots + v_p \]
An orthogonal transformation preserves total variability but redistributes it. PCA finds the transformation that concentrates variance in the first few components.
See Section 52.9.5 for a complete explanation with examples.
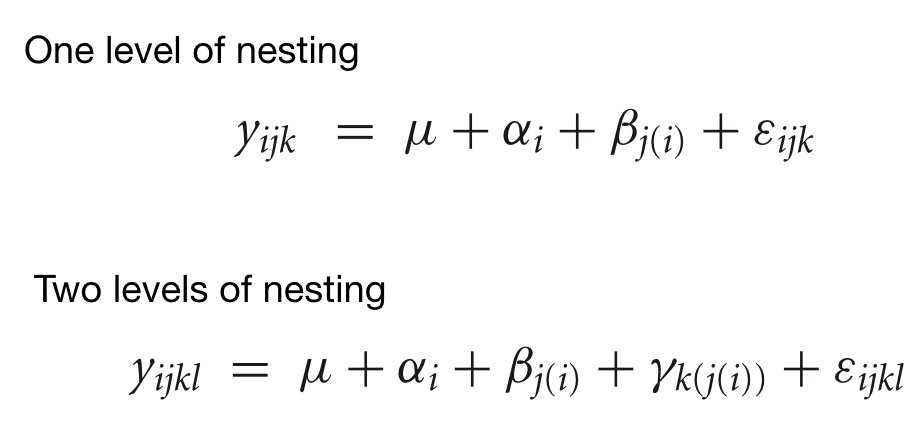# PCA on iris data
iris_pca <- prcomp(iris[, 1:4], scale. = TRUE)
# Variance explained
summary(iris_pca)Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion 0.7296 0.9581 0.99482 1.00000# Scree plot
par(mfrow = c(1, 2))
plot(iris_pca, type = "l", main = "Scree Plot")
# PC scores colored by species
plot(iris_pca$x[, 1:2],
col = c("red", "green", "blue")[iris$Species],
pch = 19, xlab = "PC1", ylab = "PC2",
main = "PCA of Iris Data")
legend("topright", levels(iris$Species),
col = c("red", "green", "blue"), pch = 19)
Each principal component is defined by its loadings—the coefficients showing how much each original variable contributes:
# Loadings (rotation matrix)
iris_pca$rotation PC1 PC2 PC3 PC4
Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863
Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096
Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492
Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971Large absolute loadings indicate that a variable strongly influences that component. The sign indicates the direction of the relationship.
Key elements of PCA output:
The first few PCs often capture most of the meaningful variation, allowing you to reduce many variables to just 2-3 for visualization and analysis.
Common approaches:
A biplot shows both observations (scores) and variables (loadings) on the same plot:
biplot(iris_pca, col = c("gray50", "red"), cex = 0.7,
main = "PCA Biplot of Iris Data")
Arrows show variable loadings—their direction and length indicate how each variable relates to the principal components.
The real power of PCA becomes apparent with truly high-dimensional data. The MNIST dataset of handwritten digits has 784 features (28×28 pixels). Can we reduce this dimensionality while preserving useful information?
library(dslabs)
if (!exists("mnist")) mnist <- read_mnist()Because pixels near each other on the image grid are correlated, we expect dimension reduction to work well:
col_means <- colMeans(mnist$test$images)
pca <- prcomp(mnist$train$images)
# Scree plot
pc <- 1:ncol(mnist$test$images)
qplot(pc[1:50], pca$sdev[1:50], geom = "line") +
labs(x = "Principal Component", y = "Standard Deviation",
title = "MNIST Scree Plot (first 50 PCs)")
The first few PCs capture substantial variance:
summary(pca)$importance[, 1:5] PC1 PC2 PC3 PC4 PC5
Standard deviation 576.82291 493.23822 459.89930 429.85624 408.56680
Proportion of Variance 0.09705 0.07096 0.06169 0.05389 0.04869
Cumulative Proportion 0.09705 0.16801 0.22970 0.28359 0.33228Even with just two dimensions, we can see structure related to digit class:
data.frame(PC1 = pca$x[, 1], PC2 = pca$x[, 2],
label = factor(mnist$train$label)) %>%
sample_n(2000) %>%
ggplot(aes(PC1, PC2, fill = label)) +
geom_point(cex = 3, pch = 21, alpha = 0.7) +
labs(title = "MNIST Digits in PC Space")
We can visualize what each PC “looks for” by reshaping the loadings back to the 28×28 grid:
library(RColorBrewer)
tmp <- lapply(1:4, function(i) {
expand.grid(Row = 1:28, Column = 1:28) %>%
mutate(id = i, label = paste0("PC", i),
value = pca$rotation[, i])
})
tmp <- Reduce(rbind, tmp)
tmp %>%
ggplot(aes(Row, Column, fill = value)) +
geom_raster() +
scale_y_reverse() +
scale_fill_gradientn(colors = brewer.pal(9, "RdBu")) +
facet_wrap(~label, nrow = 1) +
theme_minimal() +
labs(title = "PCA Loadings as Images")
PCA can reduce model complexity while maintaining predictive performance. Let’s use 36 PCs (explaining ~80% of variance) for kNN classification:
library(caret)
k <- 36
x_train <- pca$x[, 1:k]
y <- factor(mnist$train$labels)
fit <- knn3(x_train, y)
# Transform test set using training PCA
x_test <- sweep(mnist$test$images, 2, col_means) %*% pca$rotation
x_test <- x_test[, 1:k]
# Predict and evaluate
y_hat <- predict(fit, x_test, type = "class")
confusionMatrix(y_hat, factor(mnist$test$labels))$overall["Accuracy"]Accuracy
0.9751 With just 36 dimensions (instead of 784), we achieve excellent accuracy. This demonstrates the power of PCA for both visualization and model simplification.
While PCA uses correlations among variables, Principal Coordinate Analysis (PCoA) (also called Metric Multidimensional Scaling) starts with a dissimilarity matrix among observations. This is valuable when:
# PCoA example using Euclidean distances
dist_matrix <- dist(iris[, 1:4])
pcoa_result <- cmdscale(dist_matrix, k = 2, eig = TRUE)
# Proportion of variance explained
eig_vals <- pcoa_result$eig[pcoa_result$eig > 0]
var_explained <- eig_vals / sum(eig_vals)
cat("Variance explained by first two axes:",
round(sum(var_explained[1:2]) * 100, 1), "%\n")Variance explained by first two axes: 97.8 %# Plot
plot(pcoa_result$points,
col = c("red", "green", "blue")[iris$Species],
pch = 19,
xlab = paste0("PCoA1 (", round(var_explained[1]*100, 1), "%)"),
ylab = paste0("PCoA2 (", round(var_explained[2]*100, 1), "%)"),
main = "PCoA of Iris Data")
legend("topright", levels(iris$Species),
col = c("red", "green", "blue"), pch = 19)
NMDS is an ordination technique that preserves rank-order of distances rather than exact distances. It’s widely used in ecology because it makes no assumptions about the data distribution.
# NMDS example
library(vegan)
nmds_result <- metaMDS(iris[, 1:4], k = 2, trymax = 100, trace = FALSE)
# Stress value indicates fit (< 0.1 is good, < 0.2 is acceptable)
cat("Stress:", round(nmds_result$stress, 3), "\n")Stress: 0.038 plot(nmds_result$points,
col = c("red", "green", "blue")[iris$Species],
pch = 19, xlab = "NMDS1", ylab = "NMDS2",
main = "NMDS of Iris Data")
legend("topright", levels(iris$Species),
col = c("red", "green", "blue"), pch = 19)
PCA and metric PCoA produce scores on a ratio scale—differences between scores are meaningful. These can be used directly in linear models.
Non-metric multidimensional scaling (NMDS) produces ordinal rankings only. NMDS scores should not be used in parametric analyses like ANOVA or regression.
When you have multiple response variables and want to test for group differences, MANOVA (Multivariate Analysis of Variance) is the appropriate technique. It extends ANOVA to multiple dependent variables simultaneously.
Running separate ANOVAs on each variable:
MANOVA tests whether group centroids differ in multivariate space.
MANOVA decomposes the total multivariate variation:
\[\mathbf{T} = \mathbf{H} + \mathbf{E}\]
where:
These are matrices because we have multiple response variables.
Several test statistics exist for MANOVA, each a function of the eigenvalues of \(\mathbf{HE}^{-1}\):
| Statistic | Description |
|---|---|
| Wilks’ Lambda (Λ) | Product of 1/(1+λᵢ); most commonly used |
| Hotelling-Lawley Trace | Sum of eigenvalues |
| Pillai’s Trace | Sum of λᵢ/(1+λᵢ); most robust |
| Roy’s Largest Root | Maximum eigenvalue; most powerful but sensitive |
Pillai’s Trace is generally recommended because it’s most robust to violations of assumptions.
# MANOVA on iris data
manova_model <- manova(cbind(Sepal.Length, Sepal.Width,
Petal.Length, Petal.Width) ~ Species,
data = iris)
# Summary with different test statistics
summary(manova_model, test = "Pillai") Df Pillai approx F num Df den Df Pr(>F)
Species 2 1.1919 53.466 8 290 < 2.2e-16 ***
Residuals 147
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(manova_model, test = "Wilks") Df Wilks approx F num Df den Df Pr(>F)
Species 2 0.023439 199.15 8 288 < 2.2e-16 ***
Residuals 147
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The significant result tells us that species differ in their multivariate centroid—the combination of all four measurements.
A significant MANOVA should be followed by:
# Univariate follow-ups
summary.aov(manova_model) Response Sepal.Length :
Df Sum Sq Mean Sq F value Pr(>F)
Species 2 63.212 31.606 119.26 < 2.2e-16 ***
Residuals 147 38.956 0.265
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response Sepal.Width :
Df Sum Sq Mean Sq F value Pr(>F)
Species 2 11.345 5.6725 49.16 < 2.2e-16 ***
Residuals 147 16.962 0.1154
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response Petal.Length :
Df Sum Sq Mean Sq F value Pr(>F)
Species 2 437.10 218.551 1180.2 < 2.2e-16 ***
Residuals 147 27.22 0.185
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response Petal.Width :
Df Sum Sq Mean Sq F value Pr(>F)
Species 2 80.413 40.207 960.01 < 2.2e-16 ***
Residuals 147 6.157 0.042
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1MANOVA assumes:
Test homogeneity of covariance matrices with Box’s M test (though it’s sensitive to non-normality):
# Box's M test (requires biotools package)
# library(biotools)
# boxM(iris[, 1:4], iris$Species)Discriminant Function Analysis (DFA, also called Linear Discriminant Analysis or LDA) finds linear combinations of variables that best separate groups. It complements MANOVA by showing how groups differ.
DFA finds discriminant functions—weighted combinations of original variables—that maximize separation between groups while minimizing variation within groups.
The first discriminant function captures the most separation, the second captures remaining separation orthogonal to the first, and so on.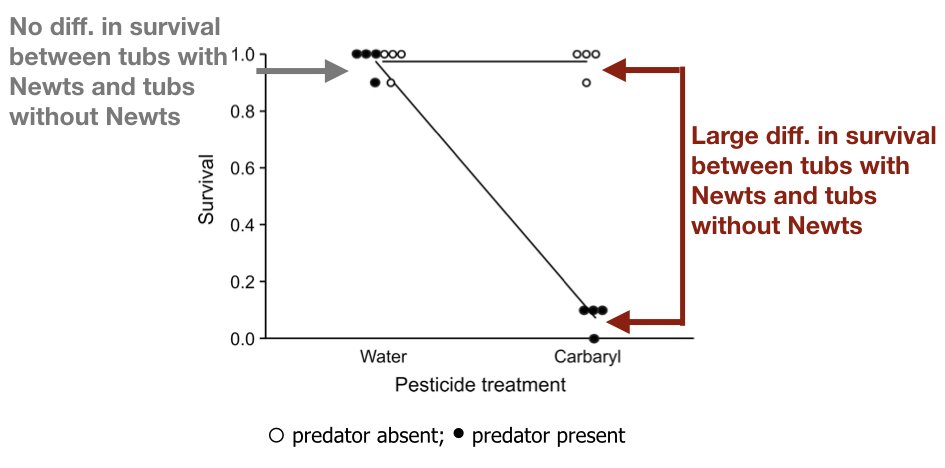
# Linear Discriminant Analysis
lda_model <- lda(Species ~ ., data = iris)
# View the model
lda_modelCall:
lda(Species ~ ., data = iris)
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa 5.006 3.428 1.462 0.246
versicolor 5.936 2.770 4.260 1.326
virginica 6.588 2.974 5.552 2.026
Coefficients of linear discriminants:
LD1 LD2
Sepal.Length 0.8293776 -0.02410215
Sepal.Width 1.5344731 -2.16452123
Petal.Length -2.2012117 0.93192121
Petal.Width -2.8104603 -2.83918785
Proportion of trace:
LD1 LD2
0.9912 0.0088 # Discriminant scores
lda_scores <- predict(lda_model)$x
# Plot
plot(lda_scores,
col = c("red", "green", "blue")[iris$Species],
pch = 19,
main = "Discriminant Function Scores",
xlab = "LD1", ylab = "LD2")
legend("topright", levels(iris$Species),
col = c("red", "green", "blue"), pch = 19)
Key components:
# Coefficients (loadings)
lda_model$scaling LD1 LD2
Sepal.Length 0.8293776 -0.02410215
Sepal.Width 1.5344731 -2.16452123
Petal.Length -2.2012117 0.93192121
Petal.Width -2.8104603 -2.83918785# Proportion of separation explained
lda_model$svd^2 / sum(lda_model$svd^2)[1] 0.991212605 0.008787395DFA can classify new observations into groups based on their discriminant scores:
# Classification accuracy
predictions <- predict(lda_model)$class
table(Predicted = predictions, Actual = iris$Species) Actual
Predicted setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 1
virginica 0 2 49# Classification accuracy
mean(predictions == iris$Species)[1] 0.98For honest estimates of classification accuracy, use leave-one-out cross-validation:
# Cross-validated LDA
lda_cv <- lda(Species ~ ., data = iris, CV = TRUE)
# Cross-validated classification table
table(Predicted = lda_cv$class, Actual = iris$Species) Actual
Predicted setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 1
virginica 0 2 49# Cross-validated accuracy
mean(lda_cv$class == iris$Species)[1] 0.98DFA is valuable for identifying which variables best distinguish groups—useful in biomarker discovery:
# Which variables contribute most to separation?
scaling_df <- data.frame(
Variable = rownames(lda_model$scaling),
LD1 = abs(lda_model$scaling[, 1]),
LD2 = abs(lda_model$scaling[, 2])
)
barplot(scaling_df$LD1, names.arg = scaling_df$Variable,
main = "Variable Contributions to LD1",
ylab = "Absolute Coefficient",
col = "steelblue")
| Method | Input | Output | Supervision | Best For |
|---|---|---|---|---|
| PCA | Variables | Continuous scores | None | Reducing correlated variables |
| PCoA | Distance matrix | Continuous scores | None | Preserving sample distances |
| NMDS | Distance matrix | Ordinal scores | None | Ecological community data |
| MANOVA | Variables + groups | Test statistics | Groups known | Testing group differences |
| DFA | Variables + groups | Discriminant scores | Groups known | Classifying observations |
For clustering methods (hierarchical, k-means) that group observations based on similarity, see Chapter 36.
PC scores and discriminant scores are legitimate new variables that can be used in downstream analysis:
This is valuable when you have many correlated variables and want to reduce dimensionality before hypothesis testing.
# Use PC scores in ANOVA
pc_scores <- data.frame(
PC1 = iris_pca$x[, 1],
PC2 = iris_pca$x[, 2],
Species = iris$Species
)
summary(aov(PC1 ~ Species, data = pc_scores)) Df Sum Sq Mean Sq F value Pr(>F)
Species 2 406.4 203.21 1051 <2e-16 ***
Residuals 147 28.4 0.19
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Explore data: Check for outliers, missing values, scaling issues
Standardize if needed: Especially important when variables are on different scales
Choose appropriate method: Based on your data type and question
Examine output: Scree plots, loadings, clustering diagnostics
Validate: Cross-validation for classification; permutation tests for significance
Interpret biologically: What do the patterns mean in your system?
tissue_gene_expression predictors by plotting them.data("tissue_gene_expression")
dim(tissue_gene_expression$x)We want to get an idea of which observations are close to each other, but the predictors are 500-dimensional so plotting is difficult. Plot the first two principal components with color representing tissue type.
The predictors for each observation are measured on the same device and experimental procedure. This introduces biases that can affect all the predictors from one observation. For each observation, compute the average across all predictors and then plot this against the first PC with color representing tissue. Report the correlation.
We see an association with the first PC and the observation averages. Redo the PCA but only after removing the center (row means).
For the first 10 PCs, make a boxplot showing the values for each tissue.
Plot the percent variance explained by PC number. Hint: use the summary function.
data("tissue_gene_expression")Compare the distance between the first two observations (both cerebellums), the 39th and 40th (both colons), and the 73rd and 74th (both endometriums). Are observations of the same tissue type closer to each other?
image function. Hint: convert the distance object to a matrix first. Does the pattern suggest that observations of the same tissue type are generally closer?The methods covered in this chapter are primarily linear dimensionality reduction techniques. PCA finds linear combinations of variables, and PCoA preserves Euclidean distances. However, biological data often lies on complex, non-linear manifolds.
For visualization of complex, non-linear structure, see Chapter 38 which covers:
These non-linear methods are particularly valuable for single-cell RNA-seq data and other high-dimensional biological datasets with complex structure.